I recently moved to the south-west of Western Australia, close to a town called Busselton. The town is famous for, among other things, the longest timber-piled jetty in the Southern Hemisphere (at 1,841m). The first time I walked the jetty I stood at the end and gazed out wondering if I could follow my gaze in a straight line where would it make landfall?

THEORY

To answer the question accurately there are two concepts worth noting. The first is that of a rhumb line — if I digitised a line (in a projected coordinate system) representing the jetty and extended that angle, it would result in a rhumb line which at the intersect point would be off to the order of a couple of hundred kilometres.

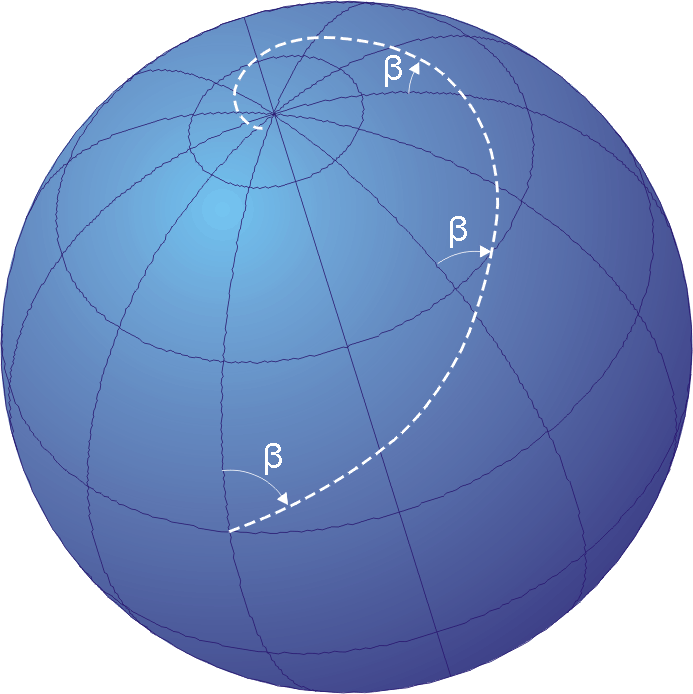
The shortest distance between any two points on the surface of the earth is the minor arc of a great circle. So if I was standing where the signpost is shown above, that is in the centre of the end of the jetty, I would need to create the minor arc of a great circle line. This would be, as the great circle wiki article states ‘analogous to “straight lines” in Euclidean geometry‘.

CREATION OF THE LINE

The process I followed to create the line was as follows:

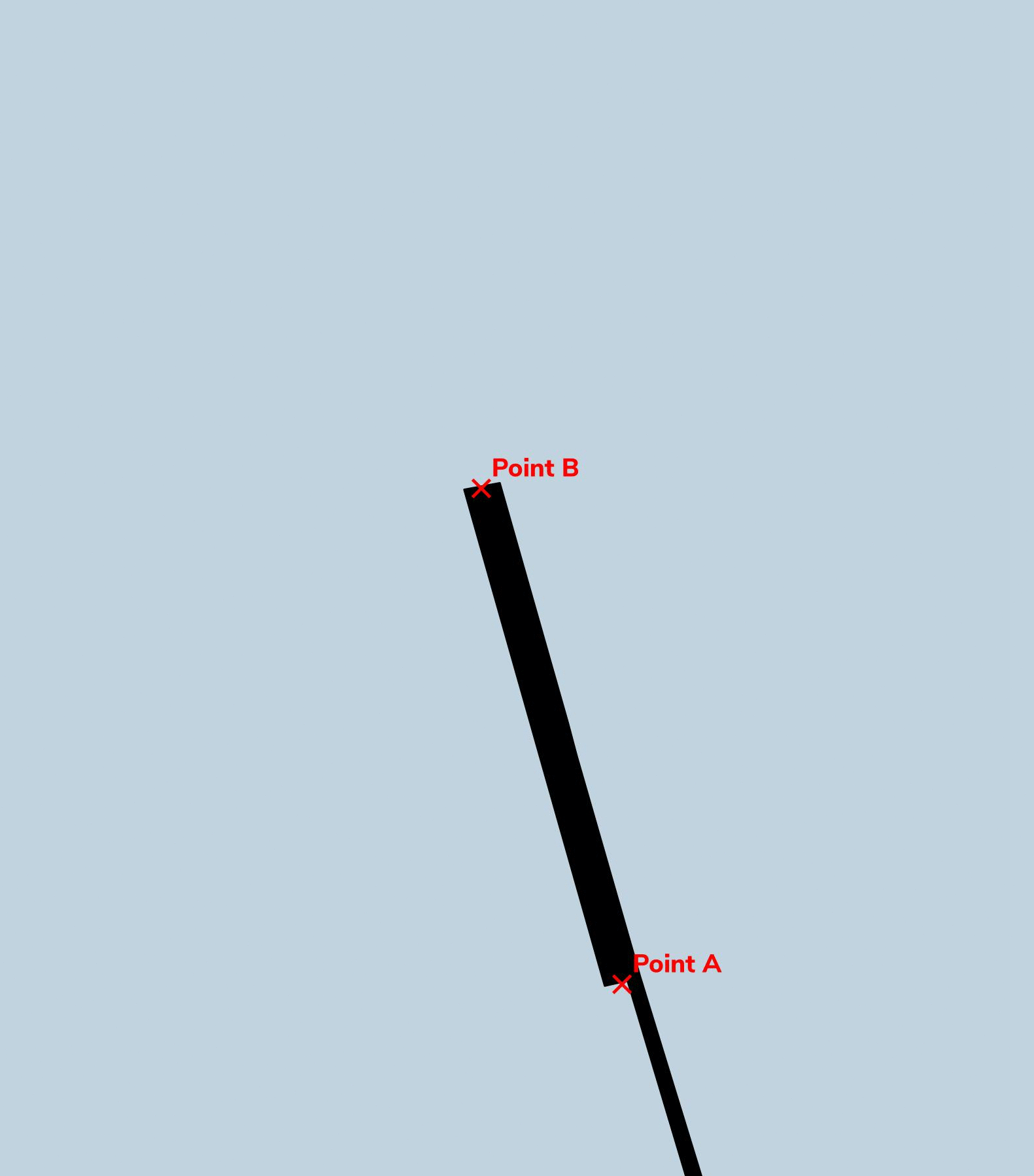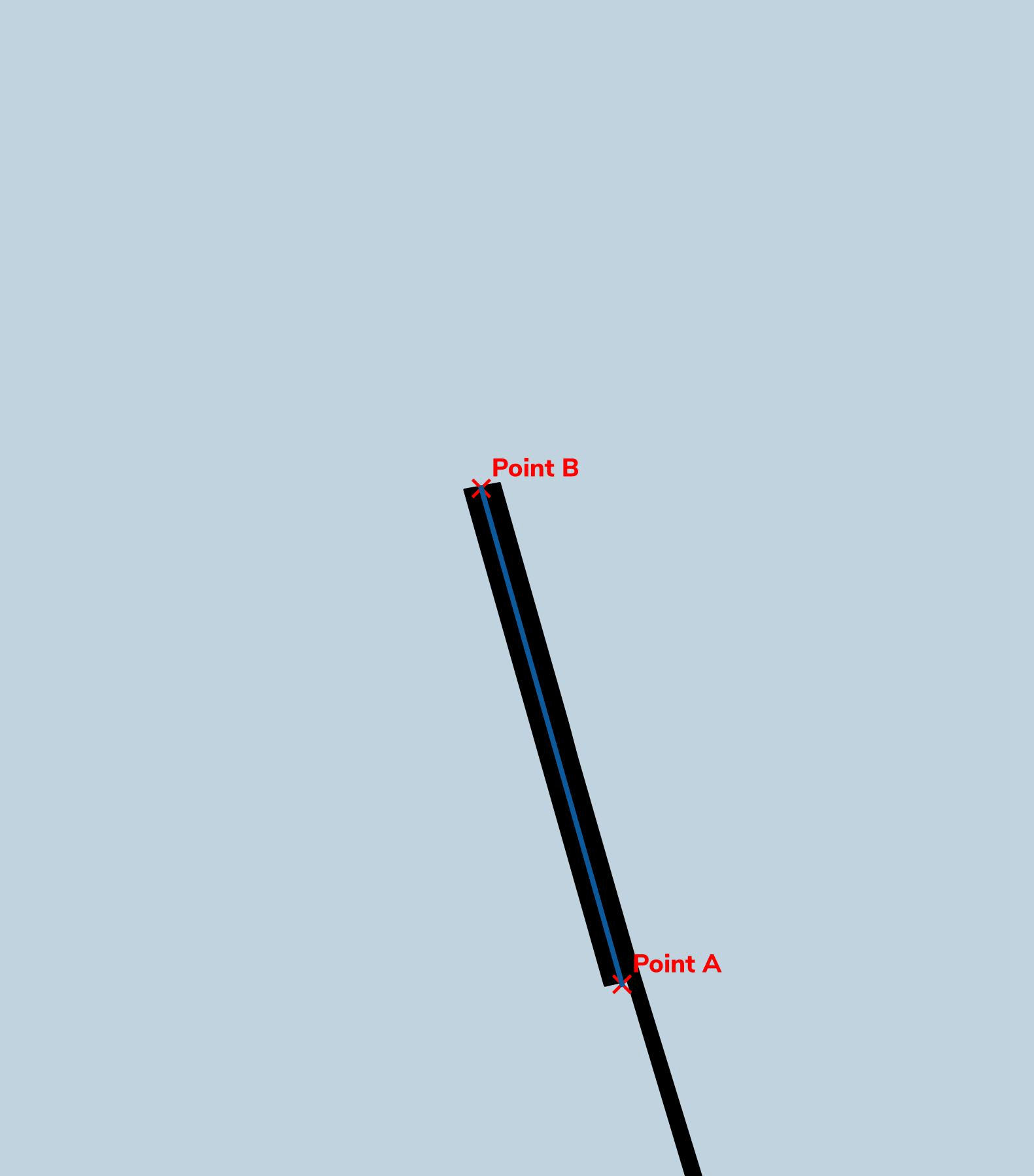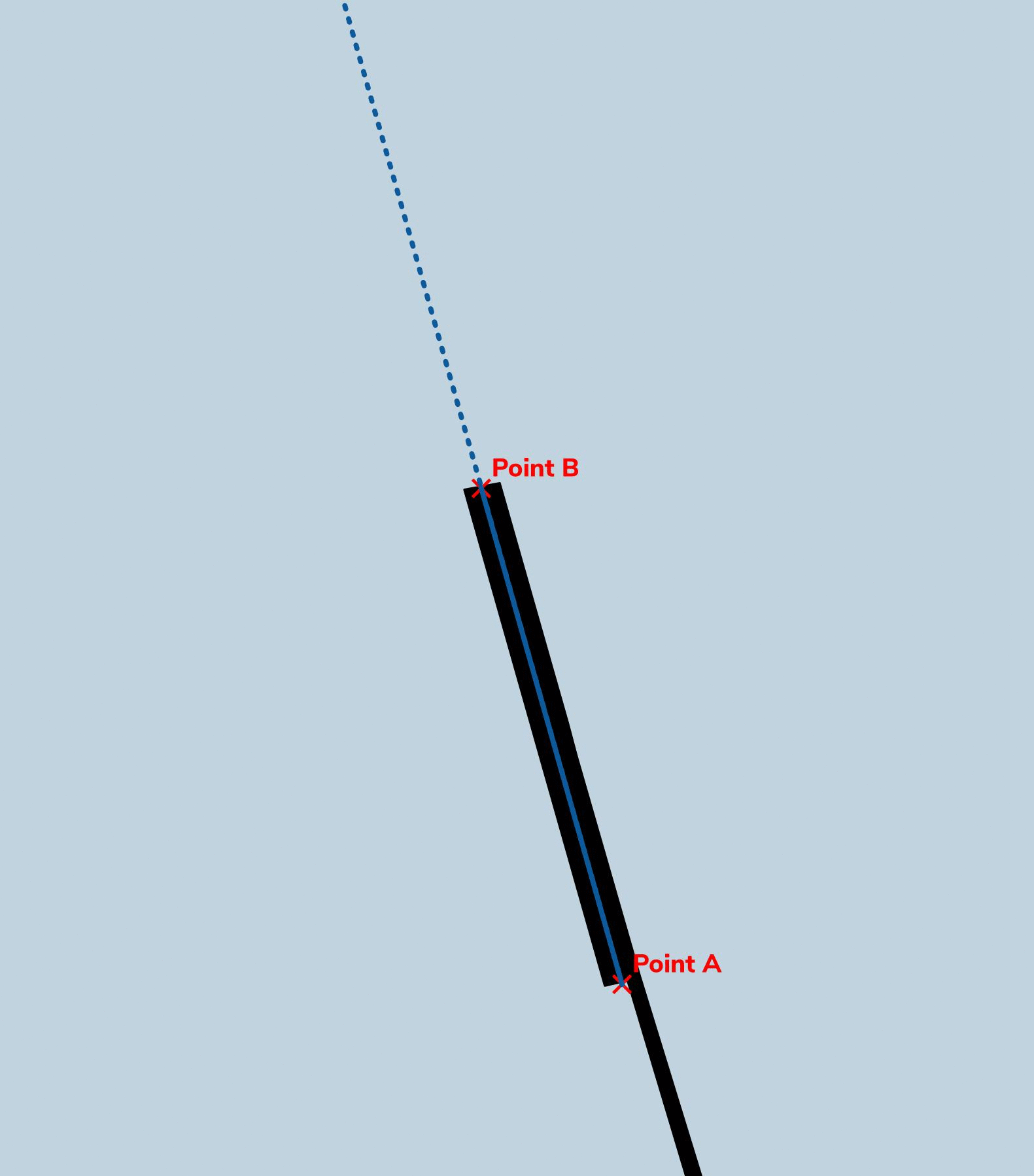
1. Create two points at the end of the jetty to represent the angle looking out.
2. Create a line between the two points.
3. Calculate the angle of the line and extend it for 1/4 the circumference of the earth at the equator.

The below GIF visualises the process-

If you’d like to carry out the same analysis yourself below is the SQL code. I’d like to thank Darrell Fuhriman for his help.

-- assume two points, calculate the angle, then extend it.
-- point 1 = -33.6307920509579, 115.338797474435  
-- point 2 = -33.6290969607648, 115.338316140276 
 SELECT
ST_Segmentize( -- break it up into segments so it looks better when re-projecting for display
    ST_MakeLine(
        ST_SetSRID(ST_Point(115.338797474435, -33.6307920509579), 4326) -- starting point (ST_MakeLine expects projected coordinates)
        ,ST_Transform(
      	ST_Project( -- find a point a long way away to use  as the second point in the line
                ST_Point(115.338797474435, -33.6307920509579)::geography -- starting point again
                ,10000000 -- 1/4 circumference of earth at the equator (should get us far enough)
                ,ST_Azimuth(ST_Point(115.338797474435, -33.6307920509579)::geography, ST_Point(115.338316140276, -33.6290969607648)::geography) -- angle between my two points
            )::geometry,
        4326)
    )::geography
,20000 -- break it into segments of 20km
);

RESULT

An imaginary line from the end of the jetty travels 802km before intersecting with Tamala, WA. It then travels for another 2,127km before meeting the district of Ayah in the Kebumen Regency in the province of Central Java, Indonesia. Where it meets land is almost equidistant between the towns of Kebasen and Kebumen (the latterhad a population of 131,750 based on the 2020 census [source]).

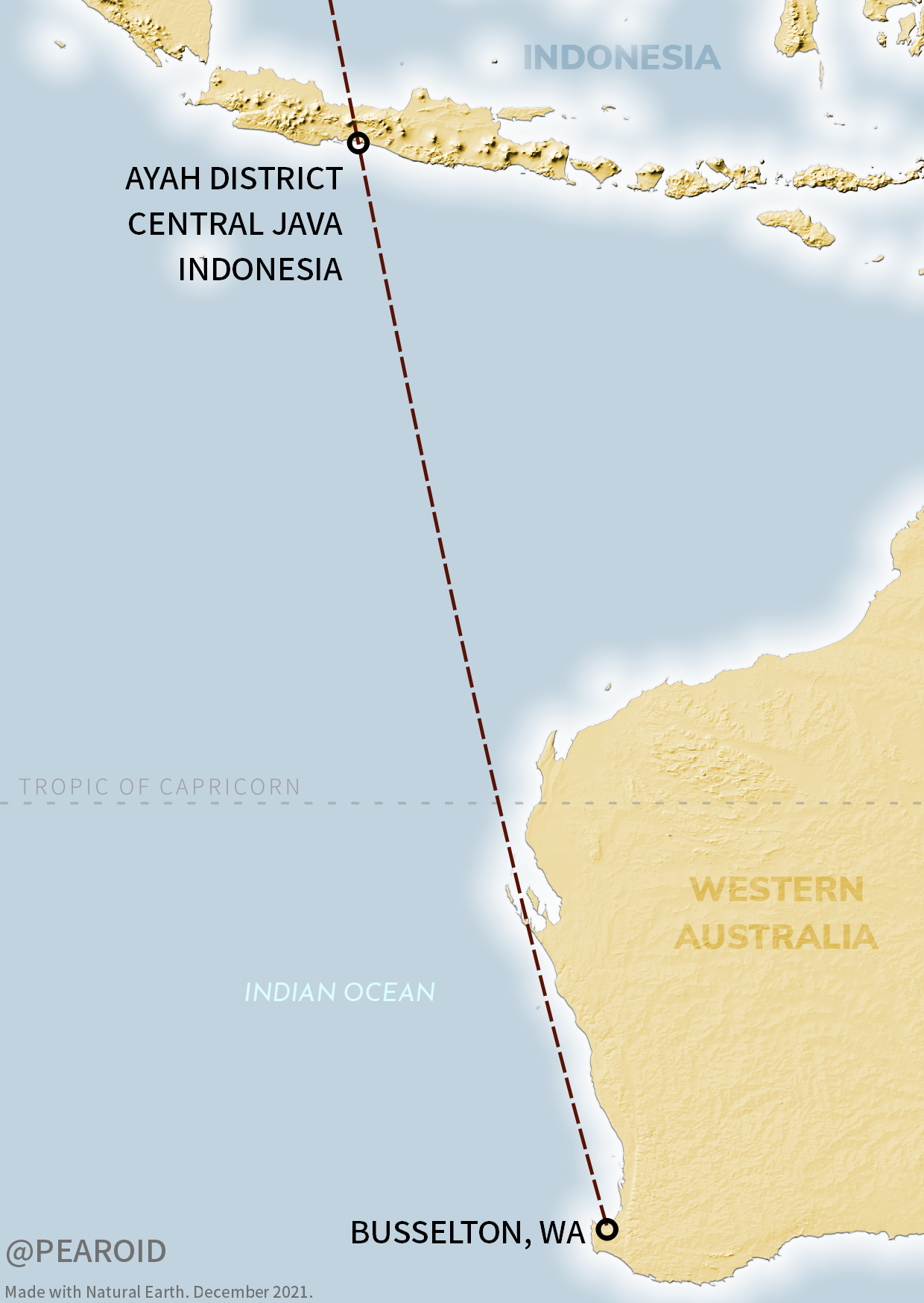
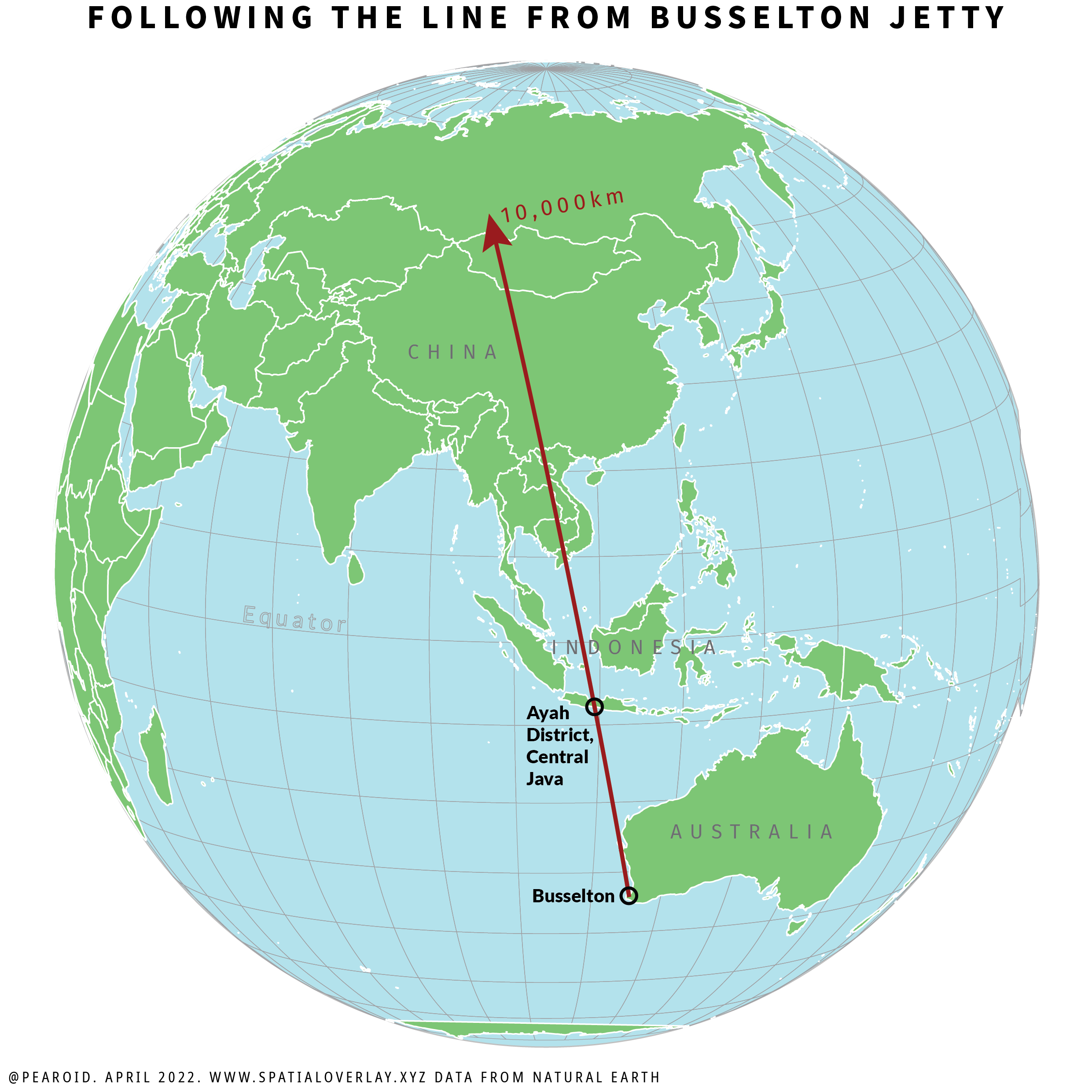
If you’re taken by the above and you ever want to travel to where it touches land in Indonesia, the coordinates are: -7.7628936, 109.4018789.